Bonjour à tous.

Ne trouvant pas de réponse satisfaisante sur Internet, je me permets de vous exposer mon questionnement.
Tout le monde parle de "Normes," de "Tableaux de câbles", de "choix obligatoires" Etc.
En réalité, je cherche à savoir calculer par les formules quelques paramètres électriques.
Mon gros souci c’est que je n’ai pas un niveau en mathématique suffisant.
Je cherche donc un "tuteur" capable de me guider pas à pas dans mes calculs.
Soyez un peu indulgent car avec l’âge je suis beaucoup moins réactif que vous.
(Ancien salarié du bâtiment, je comprends assez bien les termes techniques).
Je me suis mis dans l’idée que la longueur d’une ligne électrique influait rapidement pour le choix de la section d’un conducteur cuivre et également pour le choix du fusible ou du disjoncteur.
Je ne pose pas ces questions pour refaire une installation mais juste pour comprendre mathématiquement ce qui se passe dans les lignes électriques.
Si vous me confirmez que mes résultats ci-dessous partent dans le bon sens, je souhaiterais surement de l’aide par la suite pour savoir calculer la température dégagée dans une ligne électrique monophasée surchargée.
Pour mes calculs, je souhaite rester dans le domaine classique monophasé domestique sous gaine PVC d’une maison avec des fils de 1.5 ou 2.5 ou 4 et des fusibles de 10-20-25-32 A sous 220 V.
J’ai donc essayé de poser quelques formules sur Excel.
Je suis parti avec : Deux données fixes, U de 220 V et d’une chute de tension de 3 % de 220 V soit 6.6 V et deux données variables qui sont : la section S du fil cuivre et la longueur de la ligne L, afin de trouver la résistance R du conducteur qui me permet ensuite de trouver l’ampérage I et la puissance P.
Voici dans l’ordre les formules que j’ai posées et les résultats obtenus (avec des doutes bien sûr !)
R du fil = ( ρ x ( Lx2)) / S ρ du cuivre étant de 0.0171 et L x 2 étant la longueur du fil aller + retour.
Avec L = 28.38 m x 2 fils S = 2.5 mm² je trouve R = 0.38824 Ω donc U / R soit 6.6 V / 0.38824 = 17 A
Avec L = 30.15 m x 2 fils S = 2.5 mm² je trouve R = 0.41250 Ω donc U / R soit 6.6 V / 0.41250 = 16 A
Avec L = 32.16 m x 2 fils S = 2.5 mm² je trouve R = 0.44000 Ω donc U / R soit 6.6 V / 0.44000 = 15 A
Je vous remercie d’avance de bien vouloir me corriger les calculs ci-dessus et de m’indiquer mes erreurs.
Cordialement. R P

Bonjour RP. Votre calcul est bon (seul le premier a été vérifié directement sans calculer la résistance - mais elle doit être bonne). La méthode personnelle consiste à utiliser les unités légales, ce qui oblige à se servir des puissances de 10.
2,5 mm² = 2,5.(10 puissance -6) m² et la résistivité du cuivre = 1,71.(10puissance -8) Ω.m. Il faut un peu d'habitude pour manipuler ces grandeurs.
Par contre la longueur de la ligne au cm près n'a pas de signification physique ; on peut arrondir au mètre sans changer grand chose.
Même chose pour R = 0,38824 Ω : comment ferait-t-on pour mesurer une résistance à 10 µΩ près ?

Citation :
...savoir calculer la température dégagée dans une ligne électrique monophasée surchargée.

Cela n'a aucune utilité. Certes, on peut calculer la puissance dissipée, mais l'augmentation de température du milieu dépend du milieu lui même, des conditions de refroidissement, d'isolation. Bref, on ne fait jamais ce calcul car la norme est là pour qu'il n'y ait qu'un échauffement minime et tolérable.
Votre résultat est vérifiable avec les calculettes de chutes de tension faciles à trouver sur le net.
Une question. Quel raccourci clavier Alt(xyz) permet-il d'écrire Ω ?
Cordialement.

Bonjour GL
Réponse à GL ci-avant pour le symbole Ω avec clavier :
Clavier en position minuscule,
Touches Alt enfoncée & #8486
ou Touches Alt enfoncée Ω
------------------------------------------------------
Merci d'avoir répondu à ma question.
Je reste sur ma faim car vous aussi vous me parlez de "normes" sujet que je souhaite zapper pour l’instant.
J'ai lu et relu les normes et sans être électricien, j'en ai bien compris la bonne logique.
Pour l’utilisation des puissances je suis parfaitement d'accord avec vous. Il y a 50 ans j’étais au fond de la classe en math.
Si j'ai donné des résultats au µΩ près, c’est pour que vous puissiez vérifier si erreur ou pas de ma part.
J’ai besoin de savoir si mes formules sont bien posées car je fais souvent des erreurs avec les puissances et les décimales (une virgule mal placée et c’est le crash !).
Sur votre première ligne, vous ne me confirmez pas vraiment l'exactitude de mes calculs de débutant.
Sauriez-vous me vérifier avec précision l'ensemble des résultats ci-après ?
Avec L = 30.15 m x 2 fils et S = 2.5 mm² je trouve R = 0.41250 Ω donc U / R soit 6.6 V / 0.41250 = I = 16 A.
Si les résultats sont exacts, je cherche toujours de l’aide pour savoir s’il faut continuer avec W = R i² t pour comprendre la montée en température des fils.
Je n'ai pas trouvé de "site calculette" qui me vérifie tous ces calculs simultanément, et en plus, je pose ma formule complètement à l’envers de son utilisation courante.
Cordialement.
RP

Bonjour RP.
Pour arrondir vous pouvez modifier l'affichage dans le tableau Excel.
La résistance à température ambiante est donnée par la formule habituelle, R = ρ .l/S avec ρ en Ω.m², l en m (longueur totale des conducteurs), S en m², et le résultat en Ω.
AN : R = 1,7E-8.2.30,15/2,5E-6 = 1,7E-2.60,3/2,5 = 0,41 Ω
Pour U = 6,6 V et R = 0,41 Ω, I = U/R = 6,6/0,41 = 16,1 A.
La puissance dissipée dans la ligne = P = R.I² = U²/R = 106 W ; ramené à la longueur de la ligne cela fait 1,8 W/m ce qui n'est pas beaucoup.
Pour l'énergie dissipée, il faut multiplier par le temps (en secondes cela donne des Joules, en heures cela donne des wattheures, avec 1 Wh = 3 600 J).
Si l'énergie dissipée est dispersée dans la nature environnante, l'augmentation de température sera plus que mini. Si le système est confiné, la montée en température peut être importante.
Par exemple, un fer à souder de 30 W voire moins peut voir la température de la panne monter au dessus de 200° car l'énergie est confinée dans la panne, elle échange peu par conduction, pratiquement pas par rayonnement et convection
Merci pour le raccourci clavier.
Cordialement.

Re Bonjour GL
Un grand merci pour vos calculs, Je commence à y voir bien plus clair, Sauf si j’ai mal interprété.
Je vais essayer de joindre une capture écran pour une deuxième correction sans vouloir abuser.
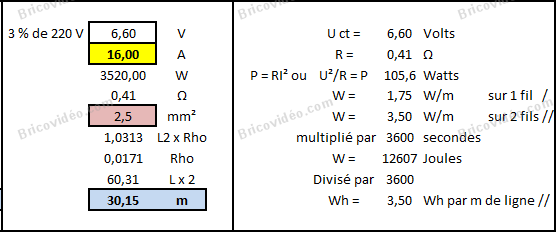
Regardez surtout le tableau de droite pour me dire si j’ai bien compris.
Merci d’avance et bon Noël.
R P

Pour agrandir l'image, cliquez dessus.

Bonjour à toutes et à tous.
Information à cet emplacement du forum électricité sera publiée l’image du jour BricoVidéo.
À ce jour 43 505 internautes bricoleurs sont inscrits sur les forums de bricolage de Bricovideo.com

Pour agrandir l'image, cliquez dessus.

Noël à Londres. Photo Patrice Faro
Si vous en avez la possibilité je vous conseille de passer les fêtes de Noël à Londres au moins une fois dans votre vie, il y a le marché de Noël très populaire, les illuminations sont super sympa dans toutes les rues. Vous pourrez profiter aussi des soldes, sur Oxford Street l'équivalent de nos Champs-Élysées à Paris les prix sont très attractifs. Si vous venez en famille avec vos enfants il faut absolument visiter le magasin de jouets Hamleys, un des plus anciens magasins de jouets du Royaume-Unis situé sur Regent Street.
Les images d'illustration proposées par BricoVidéo ne sont pas forcément en relation avec le bricolage ou le sujet traité dans ce forum.

Bonjour de nouveau pazzalarene.
Nous allons juste modifier le tableau de droite, afin que le lecteur comprenne ce qui a été fait. Donc ligne par ligne
Chute de tension choisie dans la limite des 3% autorisés Delta U = 6,6 V - Intensité choisie : 16 A
Résistance totale des deux conducteurs formant la ligne : R = 0,41 Ω
Puissance dissipée dans les deux conducteurs formant la ligne : P = R.I² = 105 6 W soit 106 W
Puissance linéique perdue dans la ligne bifilaire de 30,15 m : 1,76 W/m
Pour les deux conducteurs en parallèle, la puissance linéïque perdue est de 3,5 W/m (vérification : la ligne faisant 30,15 m, on retrouve bien 105,6 W de perdus au total)
Énergie perdue par mètre de ligne de deux conducteurs et par heure : W = 3,5 Wh.

En gros, dans votre présentation il faut préciser les hypothèses et ce qui est du domaine du calcul ; bref, ce que l'on cherche, à partir de quoi, et comment.

Pas réussi à mettre en œuvre le raccourci clavier pour Ω (ce dernier obtenu par copier-coller).
Cordialement.

Ω (ce dernier obtenu par copier-coller).
Effectivement mon raccourci clavier ne marche pas sur ce site.
Sur Word il y a deux raccourcis : Touche alt & #8486 et touche alt & #937
Toutes mes excuses !

Merci GL pour votre dernière réponse toujours aussi précise.
Je n'ose pas développer mes calculs car je ne suis pas assez sûr de moi, je débute dans ce domaine.
C'est très dangereux pour les lecteurs de lire ou de copier une formule fausse.
Encore Merci !
Cordialement. R P

Bonjour GL – Merci de regarder mes questions en Bas de page.
Chute de tension choisie dans la limite des 3% de 220V autorisés soit Delta U = 6,6V - Intensité choisie : 16A.
Je calcule la résistance totale des deux conducteurs formant la ligne : R=U / V soit 6.6 V / 16 A = 0,4125 Ω ou 0,41 Ω.
Par la formule P = U x I soit 220 V x 16 A, je trouve une puissance P de 3520 W.
Le fil déjà installé à une section de 2.5 mm².
Je cherche à savoir si la longueur de la ligne déjà installée n’est pas trop longue ?
Rho du cuivre étant de 0.017 - Avec la formule L = R x S / Rho soit 0.4125 Ω x 2.5 mm² / 0.017 = 60.66 ml de longueur de fil cuivre aller-retour / 2 = 30.33 ml de longueur de ligne.
Puissance dissipée dans les deux conducteurs formant la ligne : P = R.I² = 0,4125 Ω x 16 A² = 105.6 W de perdu au total.
Puissance linéique perdue par mètre dans 60.66 ml de fils cuivre soit 105.6 W / 60.66 ml = 1,74 W/m.
Puissance linéique perdue par mètre dans la ligne de 30,33 m soit 105.6 W / 30.33 ml = 3.48 W/m.
Énergie perdue par mètre de ligne de deux conducteurs et par heure soit 3.48 W x 3600 Secondes = 12528 Joules.
Énergie perdue par mètre de ligne de deux conducteurs et par heure soit 12528 J x 3600 Secondes = 3.48 Wh.
Question 1 : Pour les 1.74 W/m et les 3.48 W/m pouvez-vous me donner un exemple concret que je puisse ressentir comme par exemple une température ou autre chose.
Question 2 : Faut-il vraiment passer par 12528 Joules avant de trouver 3.48 Wh (Multiplié par 3600 et divisé par 3600).
Question 3 : quelle est la différence entre 3.48 W/m et 3.48 Wh ?
Question 4 : Avez-vous le droit de me dire si votre métier est webmester ou si vous avez un autre métier dans le domaine électrique ?
Merci GL et à bientôt car j’ai d’autres questions.
Cordialement. R P

Bonjour.
Je me permets d'intervenir car je vois des erreurs dans les calculs et formule donnés.

Premièrement :

Citation :
La résistance à température ambiante est donnée par la formule habituelle, R = ρ .l/S avec ρ en Ω.m², l en m (longueur totale des conducteurs), S en m², et le résultat en Ω.

Il y a juste une erreur d'unité ρ n'est pas en Ω.m² mais en Ω.m.

Ensuite :

Citation :
Puissance dissipée dans les deux conducteurs formant la ligne : P = R.I² = 0,4125 Ω x 16 A² = 105.6 W de perdu au total.
Puissance linéique perdue par mètre dans 60.66 ml de fils cuivre soit 105.6 W / 60.66 ml = 1,74 W/m.
Puissance linéique perdue par mètre dans la ligne de 30,33 m soit 105.6 W / 30.33 ml = 3.48 W/m.

Vous avez calculé la résistance totale de ligne aller et retour soit 60.66m

La résistance d'une ligne de 30.33m donne 0.206Ω donc la puissance dissipée dans la ligne et de P=RI²= 0.206x16²= 52.736
Donc la puissance dissipée par mètre donne 52.736/30.33=1.74W/m.
La puissance dissipée par mètre est donc une constante.

L'énergie perdue par mètre sera elle aussi une constante.
La puissance calculée ci-dessus est une puissance instantané/m. Donc pour avoir des Wh/m il faut multiplier votre puissance instantané/m par 1h
Ce qui nous donne 1.74W/mx1h=1.74Wh/m
Sachant que 1Wh= 3600J.
Vous obtenez donc 1.74*3600= 6264J/m.
Vous obtenez pour ligne de 60.66m une énergie dissipée de 6264x66.66=379974.24J.
Cordialement.

Bonjour à tous. Il y a du boulot !
Concernant la résistivité, elle est bien en Ω.m comme précisé le 23 décembre ; une puissance 2 s'est malencontreusement glissée ultérieurement, par mauvaise relecture. Merci pour la double correction.
Réponses aux questions :
1. Suivant leur utilisation, les câbles chauffants ont une puissance linéique.de quelques dizaines de W/m. Si la résistance est bifilaire, cette puissance est ramenée à la longueur de la ligne, et non l'aller retour.
Les calculs devraient être limités à la longueur de la ligne pour éviter les confusions, car un facteur 2 incongru peut apparaitre et fausser les résultats.
2. On calcule l'énergie directement en Wh sans passer par les joules.
3. Une puissance s'exprime en W, une énergie en Wh (l'unité légale est le joule, mais on préfère le Wh pour l'application envisagée - et quand les énergies sont importantes, on utilise les multiples kWh et MWh)
4. Le site est entièrement créé et géré par Patrice.Les contributeurs ne font que cliquer aux bons endroits, non sans se tromper quelquefois par mauvaise relecture (unités, résultats, orthographe etc.) ou erreurs.

Concernant le problème posé il est traité à l'envers. Les données devraient être une longueur de ligne (aller), l'intensité désirée, et une section normalisée. Ensuite on peut calculer la chute de tension et voir si elle rentre dans la fourchette normalisée. Si c'est le cas on ne va pas plus loin ; dans le cas contraire on choisit la section supérieure et l'on vérifie de nouveau.
Mais pourquoi s'embêter à réinventer la roue alors qu'il existe des calculettes de chute de tension (sur le net, taper calculette chute tension), ou des tableaux.
Quant à la puissance perdue par mètre de ligne cela n'a pas d'importance dans le domestique et l'industriel si l'on utilise les sections prédéfinies. Dans la distribution , on minimise les puissances perdues en ligne par élévation de la tension, donc diminution des intensités.

Pour Loulou.
Les confusions proviennent du fait que le calcul utilise la longueur des conducteurs (60 m) et l'on se ramène alors à la ligne (30 m). C'est pourquoi il est préférable de donner les résultats par mètre de ligne.
La puissance calculée ci dessus est une puissance instantané/m Non, car le temps n'intervient pas.

On travaille directement en Wh par mètre de ligne et par heure.

...La résistance d'une ligne de 30.33m donne 0.206Ω ...
...Vous obtenez pour ligne de 60.66m une énergie ...
Il faut bien faire la différence entre la ligne et les conducteurs formant cette ligne ; la ligne fait bien 30 mètres ; on ne peut changer de définition en cours de route.

Ce qu'il faut retenir est que quand on utilise la section normalisée pour les conducteurs formant une ligne, la chute de tension rentre dans la fourchette autorisée, de la puissance est perdue en ligne, mais cela on le sait depuis longtemps, elle est relativement faible par rapport à la puissance transmise, l'échauffement est minime si les conditions d'emploi et de pose de la ligne sont respectées. La puissance perdue est excessivement faible par rapport à celle dissipée dans les câbles chauffants faits pour cela.

En résumé, dans le domestique on définit la section à utiliser à partir de l'intensité et de la longueur de la ligne.
On utilise une calculette de chute de tension.

Brève relecture, en espérant qu'il n'y ait pas de fautes.
Cordialement.

Bonjour à tous et merci pour vos corrections (le débutant vous donne beaucoup de boulot !).
J’ai très bien saisi mon erreur d’unité pour la résistance en Ω mais j’ai besoin d’y réfléchir avant de l’intégrer définitivement dans mon petit cerveau.
Je vais bûcher un peu plus vos réponses pour les W/m les Joules et Les J/m avant d’affirmer que j’ai très bien compris.
Cordialement.

Réponse à GL
Selon votre réponse me disant que je traite le problème à l’envers, je vous précise que par mon calcul je voudrais connaitre la longueur maximale autorisée d’une ligne en 2.5 mm² avec un fusible de 16 A et comprendre ce qui se passe concrètement et mathématiquement si je rallonge cette ligne de x mètres.
Je vous soumets le problème d’une autre façon :
Je fais intervenir un électricien à mon domicile et je lui demande de rallonger de 20 m une ligne électrique existante sans changer la partie existante (fil de 2.5 mm² avec fusible de 16 A) pour alimenter un appareil fictif de 3520 W à 3680 W.
Question 1 : Comment va-t-il réagir et quelles questions va-t-il se poser ?
Question 2 : (si ligne existante de 31 ml à rallonger de 20 ml) comment va-t-il trouver mathématiquement la bonne solution ?
Question 3 : Comment va-t-il trouver la longueur de la ligne existante si elle est invisible ?
Question 4 : Comment font les électriciens pour installer des lignes électriques dans une immense demeure avec des longueurs de câble excessives dépassant celles d’une habitation traditionnelle ?
Pensez-vous que les électriciens se fient seulement aux tableaux ou abaques de câbles ?
J’arrive très bien à lire les abaques des câbles mais ça me gêne de ne pas sentir ce qui se passe concrètement dans les fils !
Merci pour votre patience.
Cordialement.

OK. Le plus simplement possible.
En utilisant une calculette du net : 16 A dans une ligne monophasée de 2,5 mm² de 20 m provoque une chute de tension de 5,9 V, soit 2,5 % par rapport à 230 V. Pour une ligne de 23 m, on trouve 2,94 %. Donc dans les conditions de vos hypothèses, 25 m est la longueur maximum de la ligne éclairage.
Sachant que le calibre maximum de la protection surintensité est 20 A, la même calculette donne 7,36 V soit 3,2 % ; ce qui est supérieur à la limite autorisée pour l'éclairage. Mais comme une ligne est rarement utilisée au maximum de ses possibilités, à 0,2 % près l'écart est tolérable.

En se mettant à la place de l'électricien
1. Il mesure l'intensité passant dans le circuit, il mesure la tension au départ de la ligne et aux bornes de la charge en bout de ligne et déduit si la chute de tension est acceptable ou non.
2. Il ne fait pas de maths car ce n'est ni son habitude, ni sa fonction. Il compte sur son expérience.
3. Il ne cherche pas la longueur et refait les manipulations de la réponse 1. Il peut évaluer la longueur de ligne à la louche à partir de ce qu'il voit, et des trajets supposés des lignes.
4. Pas de réponse circonstanciée par manque d'expérience dans les châteaux ou demeures un peu grandes. Il peut surdimensionner certaines sections, ou bien poser des tableaux secondaires alimentés à partir du tableau principal.

Un chargé de clientèle dans une grande entreprise peut sous-traiter les calculs de ligne. Un artisan se fiera certainement à son expérience et surdimensionnera les sections d'une façon ou d'une autre. Utilisera-t-il abaque ou calculette ? Pas d'idée. Mais il vaudrait mieux, pour ne pas surdimensionner à outrance.
Le lecteur très courant pourra refaire les calculs s'il a du temps de libre comme on l'a fait au début de ce thème.
Conclusion : 16 A (charge résistive), 2,5 mm² ligne de cuivre, 25 m maximum pour l'éclairage, et 39 m pour des usages autres que l'éclairage (chute de tension de 5 %).
Cordialement.

La calculette du net utilise une résistivité du cuivre légèrement supérieure, ce qui sous estime les longueurs calculées.

Bonne année GL !
Sur les chapitres 6 et 8, je croyais que mes formules de calculs perso étaient bonnes car je trouvais des résultats identiques à certaines calculettes d'internet.
Quand je vois vos résultats sur votre dernière réponse, je ne comprends plus rien !
Suivant le sens de mes calculs, je dois faire de grosses erreurs.
Pouvez-vous s'il vous plait me donner le lien du site concernant votre calculette.
Merci de me réécrire votre conclusion de fin de chapitre avec toutes les données pour les deux cas de 25 m et de 39 m.
Cordialement.

Bonjour pazzalarene, et merci pour vos voeux ; recevez ceux d'un modeste contributeur qui ne sait plus où donner de la résistivité !
En effet, suivant la valeur choisie, les résultats de la chute de tension peuvent légèrement différer, mais restent du même ordre de grandeur.
Si l'on veut pinailler, il faut tenir compte de la température car le cuivre comme l'aluminium sont des matériaux à coefficient de température positifs.
Ainsi, à 0°C, la résistivité du cuivre est 1,6.10-8 Ω.m ; on passera pour le moment sur la valeur du coefficient de température. C'est ainsi que vous prenez 1,7 10-8 Ω.m, en général pour les températures usuelles 1,8 10-8 Ω.m est une valeur courante, et la calculette utilise 2,3 10-8 Ω.m, valeur pour à peu près 100°C. C'est pourquoi il y a des fluctuations possibles dans les valeurs trouvées pour les résistances.
Entre 0°C et 100°C la résistivité est multipliée par 1,4 environ.
Pour 25 m et 39 m vous rentrez ces valeurs, ainsi que la section de cuivre de 2,5 mm². On prend cosinus(phi) = 1 et sinus(phi) = 0, cas du récepteur résistif pur.; la tension d'origine de la ligne est choisie à 230 V.
Vous remarquerez qu'en monophasé il faut introduire un coefficient 2, qui permet de prendre en compte la longueur totale du conducteur, le double de la longueur de la ligne.
Vous regardez tout cela. Il n'y a pas d'erreur, juste des différences suivant la valeur de la résistivité choisie.
Pour terminer, il faudrait prendre une valeur maximum de la température du cuivre de 60°C, soit une résistivité d'environ 2 Ω.m.
Cordialement.

Bonjour GL.
J'ai changé dans mes formules la valeur de Rho.
Avec 18, ça colle parfaitement avec la calculette de Volta électricité.
Merci beaucoup pour votre résistivité.
Il me reste à comprendre pour quels appareils sont appliqués les CT de 3 % et 5 %.
Pour ne plus vous embêter, je vais poser cette question sur ce site.
J'ai beaucoup apprécié votre aide.
Cordialement.
René

Bonjour,
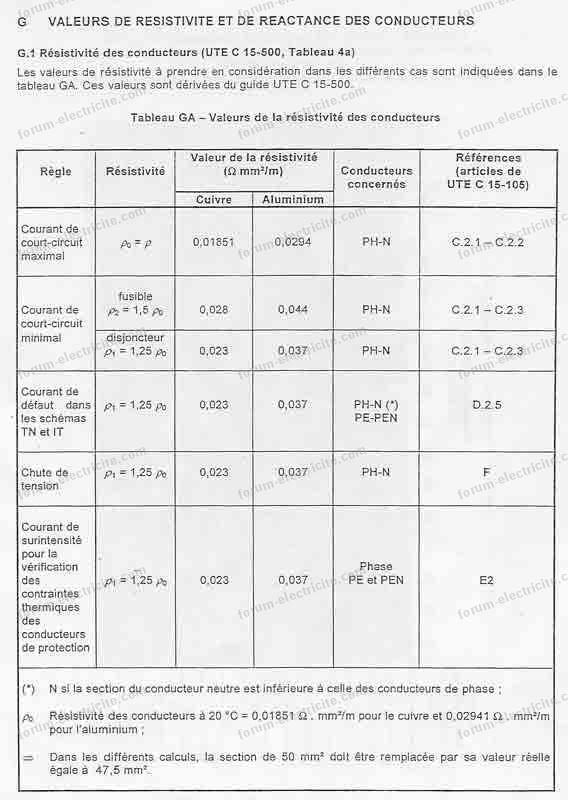
Pour complémenter voici 2 documents :
- le 1er est un tableau Excel modifiable :
- le 2ème est en extrait du guide C15-105.

chutes de tension 230v bis.xlsx

Pour agrandir l'image, cliquez dessus.